Understanding the specifications of lock-in amplifiers

From: Zurich Instruments

Posted On: 02 Nov 2023

Today, lock-in amplifiers are widespread instruments used to measure small signals buried in noise. Thanks to their versatility, they can be tailored to different experiments and address a large variety of applications. From optics and photonics to impedance analysis, they are present in many research and development labs, helping researchers and engineers to run faster and more precise experiments.

To find the instrument that best suits your needs, it is important to understand the specifications of a lock-in amplifier. While the focus of this blog post is on hardware specifications, you should keep in mind that software analysis tools and features are an equally relevant part of the measurement setup.

In this blog post, we will look closely at the following specifications:

• Instrument frequency range (input/output)
• Sampling rate and vertical resolution
• Sensitivity
• Input voltage noise
• Dynamic reserve
• Demodulation bandwidth and time constant

Instrument Frequency Range (Input/Output)

The instrument frequency range defines the range of frequencies that a lock-in amplifier can correctly analyze and use to demodulate an input signal. All of Zurich Instruments’ lock-in amplifiers can handle signals spanning from DC (0 Hz) to the maximum frequency rating of the considered instrument:

• MFLI: DC – 500 kHz
• MFLI: DC – 5 MHz
• HF2LI: DC – 50 MHz
• UHFLI: DC – 600 MHz
• GHFLI: DC – 1.8 GHz
• SHFLI: DC – 8.5 GHz

Additionally, our instruments are equipped with signal outputs – one or two per instrument, depending on the device – able to generate sinusoidal signals with a frequency that can be freely chosen within the instrument’s frequency range.

With the UHFLI, and in the future with the GHFLI and SHFLI too, it is possible to output not only sinusoidal signals but also arbitrary waveforms when using the UHF-AWG Arbitrary Waveform Generator option.

Figure 1: Landscape of Zurich Instruments Lock-in Amplifiers with their maximum input/output frequency. The 5 MHz MFLI Lock-in Amplifier is available either as a firmware upgrade to the 500 kHz variant or as a standalone instrument.

Sampling Rate and Vertical Resolution

Lock-in amplifiers measure analog signals. However, modern lock-in amplifiers (such as Zurich Instruments’) carry out all operations in the digital domain thanks to field-programmable gate array (FPGA) technology and digital signal processing (DSP) techniques. Therefore, an essential component for lock-in amplifiers is the Analog to Digital Converter (ADC), whose purpose is to convert the analog input signal to the digital domain by sampling it and digitizing it with a given sampling rate and vertical resolution, respectively. Let’s have a closer look at these two parameters.

Sampling rate

The sampling rate of an instrument indicates how many times per second the ADC samples the input analog signal. According to the Nyquist theorem, to correctly resolve a continuous signal at a given frequency f one must sample the signal at a rate that is at least double that frequency, i.e., use a sampling rate of 2f. If this requirement is not met, the original signal cannot be properly reconstructed due to artifacts such as aliasing. The effect of improper sampling can be seen in Figure 2, where a signal at a given frequency can be aliased if sampled with a sampling rate that’s too low.

For example, the HF2LI has a sampling rate of 210 MSa/s, which is over 4 times larger than the 50 MHz maximum input frequency. The reason for this oversampling (theoretically, a sampling rate of 100 MSa/s would be enough for a 50 MHz signal) is to improve anti-aliasing performance, increase resolution, and reduce noise.

Figure 2: Illustration of different sampling rates. (a) Oscillating signal with frequency fsignal. (b)-(d) Resulting sampled points with a sampling rate corresponding to 9.2 times the signal frequency, 1.1 times the signal frequency, and equal to the signal frequency. In (c) and (d), the signal cannot be unambiguously reconstructed.

Vertical resolution

Together with sampling, the ADC transforms a continuous-time analog signal into a digital signal by digitizing it. This means that it replaces each sampled analog value with an approximation from a finite set of values. This set defines the vertical resolution and corresponds to 2n discrete values, where n is the number of bits of the ADC. For example, a 4-bit ADC converter maps its input to 2⁴ = 16 values. The effect of digitizing a signal with a larger number of bits is illustrated in Figure 3: the higher the number of bits of the ADC, the better the digitized signal reflects its original analog representation. Most commonly used ADCs accept as their input only signals within a fixed range, e.g., +/-1 V. Thus a variable gain amplifier is placed before the ADC, adjusting the input signal amplitude (usually referred to as the input range) to properly map the ADC working range. In this way, the vertical resolution is maximized by using the full bit depth of the ADC. For example, the MFLI features a 16-bit ADC and covers input ranges spanning from 3 V to 1 mV. The possibility to choose among several input ranges, together with a high vertical resolution, increases the versatility of a lock-in amplifier and allows users to maximize the performance of the instrument depending on the specific characteristics of their signal.

Figure 3: Example of digitization of an analog signal (red) and the corresponding digital output with a 3- and 4-bit digitization. In both cases, the numbers on the right-hand side illustrate the digital values over which the analog signal is mapped.

Sensitivity

The sensitivity specifies the smallest absolute signal change that can be detected by the instrument. At first it might seem like the sensitivity is limited by the vertical resolution (i.e., the number of bits), but it is actually possible to achieve higher sensitivities than the spacing between two consecutive bits by exploiting the properties of noise. Indeed, every now and then the signal amplitude on top of a background of noise will toggle the least significant bits even for very small signals. To learn more about this, take a look at the section about resolution and sensitivity in this blog post. As stated in the example considered in the blog post, the MFLI can achieve sensitivities below 1 nV even though the vertical resolution given by the ADC is 30 nV at the minimum input range of 1 mV (2 mV / 2¹⁶ = 30 nV).

Input Voltage Noise

The input noise (current or voltage) of a lock-in amplifier – and, in general, of any electronic device – is the amount of noise that the instrument adds to the measured signal connected to the instrument’s input. Assuming random noise, it is usually specified in terms of noise power spectral density (noise power per unit frequency, V²/Hz) or noise amplitude spectral density (noise amplitude per square root of frequency, V/√Hz for voltage and A/√Hz for current). Based on this definition, to calculate the total amount of noise added by the instrument to an individual measurement one needs to consider the actual demodulation bandwidth, which is set by the characteristics of the low-pass filter used to demodulate the signal. For a detailed discussion of noise characterization, you can check out this blog post.

In an ideal case, the overall noise spectrum would just comprise a component decreasing as 1/f with frequency – known as the 1/f or pink noise, inversely proportional to frequency – and a flat background (that is, white noise) past the 1/f corner frequency. The input voltage noise specification usually refers to the value of the white noise plateau. However, it is important to mention that it is challenging to keep out other spurious contributions when building real analog to digital front ends: these contributions can take the form of coherent pickups from power lines or radio and the internal clock of the instrument itself. Therefore, having a noise profile close to the ideal one is not trivial and requires a careful choice of hardware components.

Additionally, the input noise depends on the specific input range and is typically provided by the supplier for different input ranges. Often, the value for the smallest input range is used for the instrument’s specifications. Figure 4 shows a measurement of the noise spectrum of the MFLI across four frequency decades for 3 different input ranges, demonstrating an input noise as low as 2.5 nV/√Hz and a profile that almost perfectly matches the ideal one.

This measurement can be easily perfomed with any of Zurich Instruments’ lock-in amplifiers, as described in this blog post.

Figure 4: Input noise of the MFLI obtained with the Sweeper module of LabOne^® within four frequency decades from 100 Hz to 1 MHz for three input ranges: 1 mV (green), 30 mV (blue), and 100 mV (red).

While it’s true that the input noise can marginally worsen at higher input ranges, the most relevant noise figure is the one referring to the minimum input range. This is because the possibility of choosing a low input range with low input noise is crucial when measuring tiny signals with an amplitude that is close to the sensitivity of the instrument. Conversely, for large signals that go towards higher input ranges, a slightly higher input noise is – in most cases – not a limiting factor for the precision of the measurement.

Furthermore, the ability of the instrument to provide very long demodulator time constants (i.e., very narrow demodulation bandwidths) helps reject more noise. Hence, when it comes to choosing a lock-in amplifier, one needs to not only consider the specified noise figure but also the maximum demodulator constant.

Dynamic Reserve

The dynamic reserve is a measurement of the instrument’s capability to withstand disturbing signals and noise that are asynchronous, i.e., away from the reference frequency. For Zurich Instruments’ lock-in amplifiers, the dynamic reserve corresponds to the point where the relative measurement accuracy remains better than 1%. It is important to point out that there is a large variance around the definition of dynamic reserve, as different manufacturers can use different parameters for this specification, e.g. different levels of measurement accuracy, making a one-to-one comparison more difficult.

The dynamic reserve is commonly expressed in decibels (dB) as

DR=20log10⁡(Vd/Vs)

where V_d is the amplitude of the disturbance and V_s the amplitude of the signal of interest.

Figure 5: Illustration of the dynamic reserve.

Zurich Instruments’ lock-in amplifiers offer dynamic reserves up to 120 dB. For example, this means that they can measure down to 1% accuracy a 10 nV signal at the reference frequency in the presence of a 10 mV spurious signal at another frequency. Of course, the specified dynamic reserve is not accessible for all signal amplitudes. This is because the input amplifier response is linear only over a certain scale, usually on the order of a few volts. Hence, a dynamic reserve of 100 dB would not be possible for, say, a 100 mV signal amplitude as this would require a 10 kV input range.

Undoubtedly, it is also important to mention that the actual dynamic reserve depends on the noise’s frequency. If the noise source happens to be synchronous with the signal (in other words, noise and signal are at exactly the same frequency), the dynamic reserve collapses to 0 dB as this noise will not be attenuated by the low-pass filter. Moving away from the demodulation frequency, the rate at which the dynamic reserve improves depends on the low-pass filter bandwidth and roll-off. Therefore, the specified dynamic reserve only refers to the reserve level for noise sources sufficiently far away from the demodulation frequency. This is also the reason why having higher-order filters that provide a steeper roll-off is essential: it ensures higher rejection of noise sources that lie in the vicinity of the demodulation frequency.

Importantly, the concepts of dynamic reserve and dynamic range are distinct. The dynamic range refers to the ratio between the maximum and minimum detectable signal by the instrument; for lock-in amplifiers, however, the more relevant specification happens to be the dynamic reserve.  

Demodulation Bandwidth and Time Constant

The demodulation bandwidth of a lock-in amplifier corresponds to the 3 dB cut-off bandwidth of the demodulators’ low-pass filter. The 3 dB cut-off bandwidth of the filter is defined as the frequency at which the output power is reduced by a factor of 2 compared to the input amplitude following the equation below:

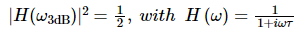
where H(w) represents the frequency response (see Figure 6, left panel) and T the time constant of the low-pass filter. The time constant is a parameter used to interpret the filter response in the time domain, and it indicates the time it takes to reach a defined percentage of the final value. It is related to the cut-off bandwidth via the formula:

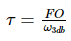
Please note that different manufacturers may use different definitions of the time constant and the cut-off bandwidth or different filter types – Zurich Instruments’ lock-in amplifiers use Butterworth filters – and thus the effective demodulation bandwidths might not be directly comparable.

A low-pass filter with a large bandwidth allows more frequency components to pass through the filter, thus making it more responsive and faster to react to signal changes (see Figure 6, right panel). A high demodulation bandwidth is important for tandem demodulation techniques, where the lower modulation frequency needs to pass through the first low-pass filter to be later detected by the second demodulator (as discussed in this blog post on amplitude-modulated signals, for example). At the same time, such higher responsiveness comes at the price of worse noise rejection as more noise components can leak through the filter. Vice versa, a filter with a very narrow bandwidth can reject more noise but it needs more time to respond when a change occurs in the measured signal.

To allow users to find the best compromise between measurement speed and noise rejection, a wide range of demodulation bandwidths and available filter orders is an important specification for a lock-in amplifier. Depending on the instrument, Zurich Instruments’ lock-in amplifiers can achieve demodulation bandwidths ranging from 300 uHz up to 11 MHz.

Figure 6: Time-domain (right) and frequency-domain (left) response functions of low-pass filters with different 3 dB cut-off bandwidths.

Two other key aspects related to the demodulation bandwidth are the maximum demodulator data transfer rate and the auxiliary output digital to analog conversion (DAC). The former refers to the speed at which the measurement results are sampled and can be saved, and it must follow the same principles described in the section about sampling rates. Essentially, to stream a signal with a chosen demodulation bandwidth the corresponding data rate should be set to be 5-10 times that bandwidth to resolve correctly all frequency components of the demodulated signal. More details on this topic can be found in this blog post. The output DAC is relevant when internal digital signals (e.g. X, Y, R or theta components from the demodulators) need to be available as analog signals and are routed out from the instruments via auxiliary output connectors. Typical values for DACs on Zurich Instruments’ lock-in amplifiers are 16- and 18-bit, with output sampling rates that depend on the instrument’s demodulation bandwidth.

Finally, it is important to stress that the minimum demodulation bandwidth is also an essential specification. As discussed in the section about input voltage noise, the possibility of choosing very narrow demodulation bandwidths can really help resolve smaller signals by rejecting more noise.

Conclusion

In this blog post, we have delved into the meaning of the most important specifications for a lock-in amplifier. These specifications define the capabilities of a lock-in amplifier; I hope this post will help you compare different instruments. When choosing the best instrument for your particular application, don’t forget other features such as the user-friendliness of the software interface, the availability of additional analysis tools such as a built-in oscilloscope, and the possibility to perform more advanced measurements such as measuring several frequencies simultaneously.